Ejercicios de las Leyes de Kepler

1) Calcular cual es el período orbital del planeta Venus, sabiendo que su distancia al Sol es de 0,72 unidades astronómicas. Recuerden que una unidad astronómica es la distancia que separa a la Tierra del Sol y equivale a 149,6 millones de Kilómetros. 

 T12  =   a13                T: período (años)
  T22       a23               a: distancia de la órbita (unidad astronómica)


12 =  13
x2   0,723   


x2 =  0,373248         x =    0,373248            


3) Datos de los planetas del Sistema Solar, utilizando las leyes del movimiento planetario propuestas por Kepler.

a)
      12 =  13
      x2   0,38713

 x2 =  0,058

 x =    0,058

 x =  0, 2408

Leyes de Kepler

Primera Ley

 Los planetas describen órbitas elípticas estando el Sol en uno de sus focos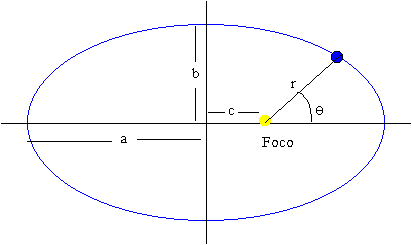

r₁ es la distancia más cercana al foco (cuando q=0) y r₂ es la distancia más alejada del foco (cuando q=p).
Una elipse es una figura geométrica que tiene las siguientes características:

• Semieje mayor a=(r₂+r₁)/2
• Semieje menor b
• Semidistancia focal c=(r₂-r₁)/2
• La relación entre los semiejes es a²=b²+c²
• La excentricidad se define como el cociente e=c/a=(r₂-r₁)/(r₂+r₁)

Segunda ley 

El vector posición de cualquier planeta respecto del Sol, barre áreas iguales de la elipse en tiempos iguales.
La ley de las áreas es equivalente a la constancia del momento angular, es decir, cuando el planeta está más alejado del Sol (afelio) su velocidad es menor que cuando está más cercano al Sol (perihelio). En el afelio y en el perihelio, el momento angular Les el producto de la masa del planeta, por su velocidad y por su distancia al centro del Sol.

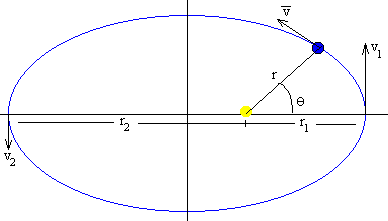
L=mr₁·v₁=mr₂·v₂

 Tercera ley

Los cuadrados de los periodos P de revolución son proporcionales a los cubos de los semiejes mayores a de la elipse.
P²=k·a³
Como podemos apreciar, el periodo de los planetas depende solamente del eje mayor de la elipse. Los tres planetas de la animación tienen el mismo eje mayor 2a=6 unidades, por tanto, tienen el mismo periodo.

Biografía de Johannes Kepler

Johannes Kepler (Weil der Stadt, Alemania, 27 de diciembre de 1571 - Ratisbona, Alemania, 15 de noviembre de 1630), figura clave en la revolución científica, astrónomo y matemático alemán; fundamentalmente conocido por sus leyes sobre el movimiento de los planetas en su órbita alrededor del Sol. Fue colaborador de Tycho Brahe, a quien sustituyó como matemático imperial de Rodolfo II.

En 1935 la UAI decidió en su honor llamarle «Kepler» a un astroblema lunar.¹

Origen y Evolución del Sistema Solar

• CONOCIMIENTOS SOBRE EL MUNDO

Los antiguos griegos fueron considerados como los primeros en utilizar una concepción científica del mundo. Llena de muchos hombres que marcaron a pasos agigantados un desarrollo para aquel mundo y para el nuestro. Con sus grandes filósofos, se pudo concebir una idea del hombre, de la vida, de la creación del Universo, pero sobre todo se pudo desarrollar una idea del ser y para que ser.

• CONOCIMIENTOS DE LOS ANTIGUOS GRIEGOS

-Tierra plana
Al principio de la antigüedad clásica, la creencia generalizada consistía en que la Tierra era plana. Los filósofos griegos de ese periodo tenían tendencia a sacar conclusiones similares a las de Anaximandro, quien creía que la Tierra era un corto cilindro con una superficie plana y circular.
Se ha conjeturado que la primera persona en haber defendido la idea de una tierra esférica fue Pitágoras (siglo VI a. C.), pero esa idea contradice el hecho de que la mayoría de los presocráticos pitagóricos consideraban que la tierra era plana.2 En su obra De Caelo, Aristóteles(siglo IV a. C.) da una explicación razonada de por qué la Tierra es una esfera y cita un valor para su circunferencia que es el correcto dentro de un factor de dos. En el siglo III a. C., Eratóstenes da una estimación más correcta de su circunferencia.3
En tiempos de Plinio el Viejo, en el siglo I, la mayoría de los estudiosos occidentales aceptaban que la Tierra tenía forma esférica. Más o menos por entonces, Claudio Ptolomeo derivó sus mapas de un globo curvado, y desarrollo el sistema de latitud, longitud, y climas. Sus escritos se convirtieron en la base de la astronomía europea durante la Edad Media, aunque la antigüedad tardía y la Alta Edad Media vieron argumentos ocasionales en favor de una Tierra plana.  

-Aportación de Pitagóricos:
La astronomía de los pitagóricos marcó un importante avance en el pensamiento científico clásico, ya que fueron los primeros en considerar la tierra como un globo que gira junto a otros planetas alrededor de un fuego central. Explicaron el orden armonioso de todas las cosas como cuerpos moviéndose de acuerdo a un esquema numérico, en una esfera de la realidad sencilla y omnicomprensiva. Como los pitagóricos pensaban que los cuerpos celestes estaban separados unos de otros por intervalos correspondientes a longitudes de cuerdas armónicas, mantenían que el movimiento de las esferas da origen a un sonido musical, la llamada armonía de las esferas.

Imágenes de ejercicios con la fórmula de la Ley de Gravitación

                                                   

Ley de Gravitación Universal

La Ley de la Gravitación Universal es una ley física clásica que describe la interacción gravitatoria entre distintos cuerpos con masa. Ésta fue presentada por Isaac Newton en su libro Philosophiae Naturalis Principia Mathematica, publicado en 1687, donde establece por primera vez una relación cuantitativa (deducida empíricamente de la observación) de la fuerza con que se atraen dos objetos con masa. Así, Newton dedujo que la fuerza con que se atraen dos cuerpos de diferente masa únicamente depende del valor de sus masas y del cuadrado de la distancia que los separa. También se observa que dicha fuerza actúa de tal forma que es como si toda la masa de cada uno de los cuerpos estuviese concentrada únicamente en su centro, es decir, es como si dichos objetos fuesen únicamente un punto, lo cual permite reducir enormemente la complejidad de las interacciones entre cuerpos complejos.
Así, con todo esto resulta que la ley de la Gravitación Universal predice que la fuerza ejercida entre dos cuerpos de masas  y  separados una distancia  es proporcional al producto de sus masas e inversamente proporcional al cuadrado de la distancia, es decir:

donde

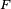 es el módulo de la fuerza ejercida entre ambos cuerpos, y su dirección se encuentra en el eje que une ambos cuerpos.

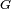 es la constante de la Gravitación Universal.

Es decir, cuanto más masivos sean los cuerpos y más cercanos se encuentren, con mayor fuerza se atraerán.

Introducción a la Ley de Gravitación Universal

• LA MANZANA DE NEWTON

Se dice que en una tarde de verano, mientras el gran físico británicoIsaac Newton  que se había refugiado en 1665 en su casa de campo de Lincolnshire, Inglaterra, de la epidemia de peste bubónica que azotaba Londres, descansaba bajo un árbol de manzana, un fruto de dicho árbol cayó al suelo.

En ese mismo instante Newton comprendió que tenía que haber “algo” que atrayera a esa manzana hacia el suelo, así comprendió y engendró la famosa ley de gravitación universal, una de las leyes que han definido nuestra historia moderna.

Hay quien piensa que es una leyenda pero la Royal Society de Londres  en conmemoración de su 350º aniversario en 2010, sacó a la luz un manuscrito original que relata como Isaac Newton, al caerse una manzana, meditó la teoría de la gravedad. Se trata de un manuscrito, del amigo y contemporáneo de Newton, el físico William Stukeley,  para una novela biográfica, “Memorias de la vida de Sir Isaac Newton” (1752), que había permanecido resguardada en los archivos de la prestigiosa institución.

Parece que el árbol original se conservó hasta 1814, cuando cayó a consecuencia de una violenta tormenta, y su madera se utilizó para hacer sillas. Por entonces ya se habían obtenido varios injertos de aquel ejemplar, y hoy existen docenas de clónicos del mismo, plantados en los jardines de distintas facultades de física de todo el mundo.

Trabajo Práctico: OPTICA

• EJERCICIOS

Espejos Esféricos 
1)
a)
     1     = 1     + 1
    1,20    0,60    x'

    - 1 = 1     - 1     
      x'    0,60   1,20

    - 1 = 5
      x'    6

     x' = - 6
             5

     x'= -1,20m

b) 

    -x = 1,20 = 2
     x     1,60
y'         = 1,20m
1,60cm   0,60

y' = 1,20m . 1,60 cm
       0,60m

y' = 3,20m ----> La persona se ve de 3,20m (tamaño)

c) Es virtual, porque la imagen se ve detrás del espejo, se forma con la prolongación de los rayos reflejados.

2)a)
      1 = 1 + 1       f     x    -30
    
     -1 = 1 + 1 cm
      f      x   -10

     1 = -1 + 1 cm
     f      x     10

-1 +  1 = 1 + 1 
x      10   x   -30
-1 - 1 = 1  -  1 
x     x    -30  10 

-2 = -2 
  x     15

x. (-2) = -2. 15

x = -2 . 15
          -2
x = 15cm -----> Distancia objeto - espejo

 b)
    1 = 1       + 1                                r = 2.f
    f     15cm   -30cm                         r = 2. 30cm
                                                        r = 60cm
    1 = 1     
    f     30cm
   
    f  = 30 cm-----> Mitad del radio

Espejos Curvos

• ESPEJOS ESFÉRICOS:

Se llama así a los espejos cuya superficie puede considerarse parte de una esfera.

Pueden ser cóncavos o convexos, según la superficie interior o exterior de la esfera.

Para estudiar los espejos esféricos se elige el eje del espejo. Se denomina vértice al punto donde dicho eje intersecta la superficie esférica. 

Se utilizan rayos muy cercanos al eje del espejo o, lo que es equivalente, espejos de poca curvatura. Esta aproximación se denomina paraxial, de acuerdo con ella son válidas las construcciones y ecuaciones que se usan.

Algunos puntos del eje de los espejos esféricos que tienen propiedades particulares, relacionadas con la forma en que se reflejan los rayos que pasan por ellos, son el foco y el centro de curvatura.

Foco: los rayos que inciden paralelos al eje, se reflejan pasando por el foco, y análogamente, si los rayos incidentes pasar por el foco, los reflejados son paralelos al eje. El foco se encuentra en el punto medio entre el centro de curvatura y el vértice.

Todos los rayos que pasan por el centro de curvatura se reflejan sobre sí mismos.

En el caso de los espejos convexos, el foco y el centro de curvatura se encuentran del lado de la superficie no reflectora. La luz no llega a esos puntos en estos espejos.

• FORMACIÓN DE IMÁGENES EN ESPEJOS ESFÉRICOS:

Para construir la imagen en los espejos esféricos se toman tres ratos particulares, llamados rayos principales:

- El que pasa por un extremo del objeto y por el centro de curvatura, que se refleja sobre sí mismo.

- El que pasa por un extremo del objeto y por el foco, que se refleja paralelo al eje,

- El que pasa por un extremo del objeto y es paralelo al eje, que se refleja pasando por el foco.

En un espejo cóncavo, si las imágenes se forman por rayos reflejados y no por prolongaciones de ratos se dice entonces que la imagen es real: se la podrá observar si se coloca una pantalla en el lugar en que se forma.

Existen tres casos: 

a) Cuando la coordenada del objeto es mayor que la del centro de curvatura: la imagen es real, invertida y menor que el objeto.

b) Cuando el objeto está entre el foco y el centro de curvatura : la imagen es real invertida y mayor que el objeto.

c) Cuando el objeto está entre el foco y el espejo: la imagen es virtual, derecha y mayor que el objeto.

En los espejos convexos, la luz no llega al foco ni al centro de curvatura. Todas las imágenes son virtuales, derechas y menos que el objeto.

Para ambos tipos de espejos esféricos, la posición y el tamaño de la imagen se relacionan con las d el objeto mediante la ecuación:

donde f es la coordenada del foco o distancia focal, x es la coordenada del objeto y x' es la coordenada de la imagen.

 La ecuación anterior se puede escribir en función del radio de curvatura, reemplazando: 

Para calcular el tamaño de la imagen se define el aumento lateral, de la siguiente manera:

 donde y es la coordenada vertical del objeto mientras que y' es la de la imagen. Para el caso de los espejos con el sistema de coordenadas elegido, vale la relación: