Primera Ley
Los planetas describen órbitas elípticas estando el Sol en uno de sus focos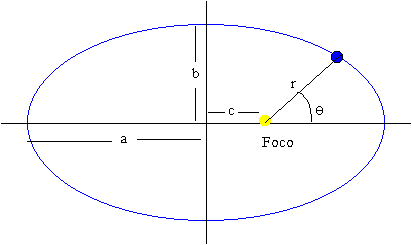
r1 es la distancia más cercana al foco (cuando q=0) y r2 es la distancia más alejada del foco (cuando q=p).
Una elipse es una figura geométrica que tiene las siguientes características:
- Semieje mayor a=(r2+r1)/2
- Semieje menor b
- Semidistancia focal c=(r2-r1)/2
- La relación entre los semiejes es a2=b2+c2
- La excentricidad se define como el cociente e=c/a=(r2-r1)/(r2+r1)
Segunda ley
El vector posición de cualquier planeta respecto del Sol, barre áreas iguales de la elipse en tiempos iguales.La ley de las áreas es equivalente a la constancia del momento angular, es decir, cuando el planeta está más alejado del Sol (afelio) su velocidad es menor que cuando está más cercano al Sol (perihelio). En el afelio y en el perihelio, el momento angular Les el producto de la masa del planeta, por su velocidad y por su distancia al centro del Sol.
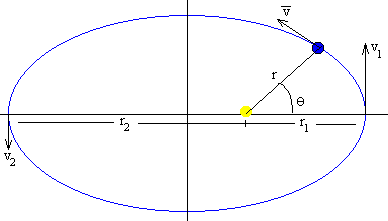
L=mr1·v1=mr2·v2
Tercera ley
Los cuadrados de los periodos P de revolución son proporcionales a los cubos de los semiejes mayores a de la elipse.P2=k·a3
Como podemos apreciar, el periodo de los planetas depende solamente del eje mayor de la elipse. Los tres planetas de la animación tienen el mismo eje mayor 2a=6 unidades, por tanto, tienen el mismo periodo.
No hay comentarios:
Publicar un comentario